Detector Technology

Low-temperature detectors

We develop detectors based on low-temperature calorimetry principles. The basic idea is to cool an absorber to near absolute zero, such that its thermal excitations are greatly suppressed. A thermometer then reads out the excitations produced when a particle interacts with the absorber. The X-ray version of these detectors are called microcalorimeters, due to their minute size compared to calorimeters used in colliders.

The Ideal Microcalorimeter

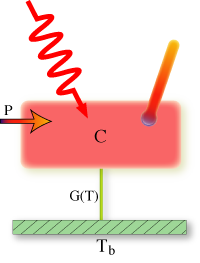
In its most simple incarnation, a microcalorimeter has three parts: an absorber with heat capacity C, a thermometer, and a weak thermal link (with conductance G) to a cold bath at temperature Tb. The cold bath is maintained by a refrigerator at cryogenic temperatures (typically from 50 to 300 millikelvin depending on the application). When a photon hits the absorber, its energy is converted into heat, which raises the temperature of the absorber. A very sensitive thermometer registers this increase in temperature. The device then cools through the weak thermal link and returns to its quiescent state, ready to detect another photon. The height of the thermal signal is proportional to the energy of the photon. The time constant of this process is determined by the heat capacity C of the absorber and the thermal conductance G of the weak link. The time constant is given by tau=C/G. With these devices we can very accurately determine the energy of the photon, its time of arrival, and by making an array of such devices and placing it at the focal plane of an imaging optic, we can also determine the direction of the photon. Thus we have a single-photon-counting imaging spectrometer.

To derive the response of a microcalorimeter to an incident photon, we start by looking at energy flowing in and out of the microcalorimeter. The change in temperature of the absorber will depend on the steady state power coming in P, the energy leaving due to the weak thermal link G, and inputs in energy from photons E:

where C is the heat capacity of the absorber, T is the temperature of the absorber, and Tb is the bath temperature. This equation can be solved for the temperature T assuming the power P is a constant:

So the response to a photon is a single exponential decay with a time constant τ= C/G and an amplitude proportional to the energy of the photon:

All we need is a good way to accurately measure the temperature of the absorber. In our lab we use a superconductor as our thermometer: the transition-edge sensor (TES).

Next: Transition-Edge Sensors